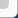Коперник. 112 элемент. Продолжение 3

Объяснить с позиций геоцентризма движение Луны значительно сложнее, чем видимое годовое движение Солнца, хотя Луна и обращается в действительности вокруг Земли. Это обусловлено наличием ряда неравенств в движении Луны, каждое из которых нуждается в особом учете.

Для построения теории движения Луны Птолемей использовал наблюдения лунных затмений, так как для них место наблюдения не имеет никакого значения: они усматриваются одновременно на всей обращенной к Луне стороне Земли. Птолемей вычислил средние суточные движения Луны по долготе (относительно точки весеннего равноденствия), по так называемой аномалии (относительно перигея лунной орбиты), по широте и по фазе (относительно Солнца).

В своей модели движения Луны Птолемей использует обе гипотезы: как гипотезу эпицикла, так и гипотезу эксцентра.

Первоначально Птолемей строит «простую» модель движения Луны, которая используется для нахождения средних скоростей движения Луны по долготе и величины разности между фактической долготой Луны и долготой, рассчитанной по средней скорости ее изменения. В этой модели он вводит понятие деферента – круга в плоскости лунной орбиты, имеющего центр в центре Земли. Плоскость деферента наклонена к плоскости эклиптики на угол в 5º, соответствующий величине максимального отклонения Луны от эклиптики по широте, и равномерно вращается против направления годового движения Солнца вокруг оси, перпендикулярной плоскости эклиптики. В этом же направлении вращается линия узлов – точек пересечения лунной орбиты с эклиптикой – с периодом обращения 18,6 лет. 

По деференту движется центр эпицикла, отношение радиуса которого к радиусу деферента определяется из последовательности лунных затмений. Центр эпицикла движется равномерно в направлении движения Солнца по эклиптике и с угловой скоростью, равной скорости движения относительно линии узлов. По эпициклу движется, наконец, Луна – равномерно и в обратном направлении с угловой скоростью, равной скорости движения по аномалии (относительно перигея лунной орбиты).

Однако «простая» модель неудовлетворительно выражала особенности движения Луны относительно Солнца. Эти особенности можно объяснить, если предположить, что расстояние центра эпицикла от центра Земли изменяется в течение лунного месяца. Чтобы добиться совпадения с наблюдаемыми явлениями, Птолемей заменяет деферент, центр которого совпадает с центром эклиптики, эксцентром, центр которого находится на неко-тором расстоянии от центра Земли. Это расстояние определяется из соотношения откло-нений движения Луны от равномерного (среднего) в апогее и перигее. 

Но и этой меры оказывается недостаточным для того, чтобы объяснить видимое движение Луны, соблюдая при этом требование равномерности круговых движений. 

К понятию экванта

Чтобы формально соблюсти это требование, Птолемей вводит для Луны, как и для планет, уравнивающую точку – эквант, из которой движение центра эпицикла по деференту усматривается как равномерное. Эта точка располагается на линии, соединяющей точки апогея и перигея планетной орбиты, и смещена от центра деферента на ту же величину, что и центр эклиптики, но в противоположном направлении. Если провести из экванта радиусы, отстоящие друг от друга на равные углы, как спицы на колесе, то они разделят деферент, центр которого в моем сравнении не совпадает с осью колеса, на дуги неравной величины: наибольшие – у перигея и наименьшие – у апогея. Для согласования предвычисляемого положения Луны или планеты подбиралось надлежащее положение центра деферента, а тем самым и экванта.

До студентов плохо доходило птолемеево понятие экванта, и Ретик обычно пояснял его рисунком. Он проводил через произвольную точку пучок лучей, отстоящих друг от друга на равные углы. А затем проводил окружность с центром не в точке пересе-чения лучей, а в смещенной относительно нее точке. Что получилось? «Лучи делили окружность на дуги неравной величины! Представьте себе, что центр окружности – это центр деферента, а точка пересечения лучей – тот самый эквант!» – говорил Ретик.

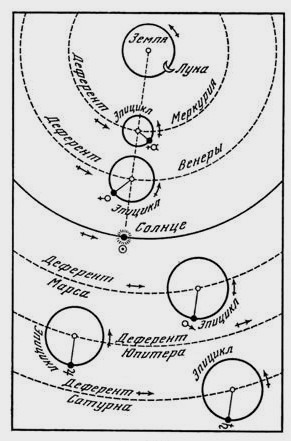
Для описания движения планет Птолемей использовал модель с деферентами и эпициклами. Чтобы учесть неравномерность изменения долготы планеты, Птолемей объясняет движение планет по долготе перемещением центра эпицикла по деференту, а по аномалии (относительно перигея планетной орбиты) – перемещением планеты по эпициклу. Вращательное движение планеты по эпициклу осуществляется в том же направлении, что и вращательное движение Солнца по эклиптике. 

Движения планет связываются с движением Солнца, но по-разному. 

Для нижних планет, не отходящих далеко от Солнца, направление с Земли на центр эпицикла всегда совпадает с направлением на Солнце. Это понятно, потому что траектория движения Меркурия и Венеры симметрична на небесном своде относительно Солнца. Полный цикл изменения долготы нижних планет совпадает с периодом обращения Солн-ца по эклиптике. Эту величину – год – Птолемей и принял за период обращения эпицик-лов Меркурия и Венеры по деференту. Период обращения планеты по эпициклу он принял равным интервалу между двумя последовательными одноименными элонгациями, что составляет для Меркурия – 88 суток, для Венеры – 225 суток. 

Деференты и эпициклы в системе Птолемея

Плоскости деферентов нижних планет совпадают с плоскостью эклиптики, плоско-сти их эпициклов наклонены к плоскости эклиптики на малые углы.

Радиусы эпициклов верхних планет всегда параллельны направлению с Земли на Солнце. Такая модель обеспечивает неизменность положения апогея наблюдаемой траектории верхней планеты относительно звезд. Для верхних планет период обращения по деференту принят равным полному циклу изменения долготы, который, по многолетним наблюдениям, составляет: для Марса – 687 дней, для Юпитера – около 12 лет, для Сатурна – около 30 лет. Период обращения по эпициклу для каждой верхней планеты – один год. Плоскости деферентов верхних планет наклонены к плоскости эклиптики на малые углы, а плоскости их эпициклов параллельны плоскости эклиптики.

В отличие от других планет, для Меркурия Птолемей вводит второй, подвижный эксцентр, центр которого обращается вокруг точки экванта. В итоге центр эпицикла Меркурия обращается относительно Земли не по окружности, а по кривой, имеющей две точки наибольшего сближения с Землей, то есть два перигея.

Для Меркурия и Венеры из сравнения углов наибольших элонгаций в апогее и перигее простым геометрическим построением Птолемей находит радиус эпицикла в долях радиуса деферента, и величину эксцентриситета – расстояния между центрами деферента и эклиптики. Для определения значений эксцентриситета и положения апогеев внешних планет Птолемей использует наблюдения их противостояний – диаметральных положений по отношению к среднему положению Солнца, и рассчитывает радиусы эпициклов этих планет.

Теория Птолемея позволяла истолковывать петлеобразные движения планет и предвычислять положения небесных светил. Она была математически безупречна, внутренне не противоречива, вполне удовлетворительно описывала наблюдаемые движения небесных светил. Если с появлением новых эмпирических данных обнаруживалось несовпадение фактических положений светил с предвычисленными, то это легко объяснялось отнюдь не пороками самой системы. Для уточнения предвычисляемой траектории светила вовсе не требовалось разрушать всю модель Птолемея с ее эксцентрами, эпициклами и эквантами, а достаточно было дополнить ее новыми эпициклами, в которых центр каждого последующего перемещался по окружности предыдущего.

И вот до Виттенберга дошла весть, что некий Николай Коперник написал тезисы, в которых отрицаются сами принципы, положенные в основу систем Аристотеля и Птолемея, и провозглашаются новые принципы, утверждающие совсем иную систему мироздания, с позиций которой просто и наглядно объясняются наиболее сложные явления в видимом движении светил.

Конечно, молодой профессор не мог пройти мимо открытия, грозившего перевернуть всю науку астрономии, и поэтому он так поспешал к берегам холодной Балтики.

*     *     *

– Вот и поезд тронулся, и до Вильнюса еще далеко, так расскажите нам лучше, Семен Борисович, не о кругах небесной сферы, а о самом Копернике, – оживился Василий Михайлович. – А вы знаете, ваш Коперник, можно сказать, был в некотором роде моим соседом. В нашем Калининграде, бывшем Кёнигсберге, есть улица Коперника. Я жил там неподалеку. Такая маленькая, что даже улицей ее называть можно лишь с большой натяжкой, так, улочка или проулочек, булыжником замощенный. И домов-то на ней по три-четыре с каждой стороны, хотя неподалеку и бывший Королевский замок, и Кафедральный собор, и река Преголя, но мало кто из жителей города о ее существовании знал. При немцах это имя – Коперникус-штрассе – носила совсем другая улица.

– Да, я знаю эту улицу, – откликнулся Семен Борисович. – А теперь, как вы предлагаете, вернемся к объекту нашего исследования.

Итак, Николай Коперник родился в 1473 году в городе Торуни, немецкое название Торн. В XV веке город был немецким торговым центром, входившим в Ганзейский союз, и находился под властью Тевтонского ордена, правившего Пруссией. За два десятка лет до рождения Николая Тевтонский орден потерпел поражение в тринадцатилетней войне с Королевством Польским, и город перешел под власть Польши. Отец будущего астронома, тоже Николай, приехал в Торунь примерно в 1460 году, по-видимому, из Кракова, хотя некоторые источники утверждают, что из Германии. Последнее утверждение никакой ясности не вносит, так как к концу XV-го века Германия была рыхлым союзом практически независимых княжеств и епископских епархий. Чаще всего отца Коперника называют купцом, но разные источники приписывают ему и другие профессии: то называют его пивоваром, то крестьянином, то булочником и даже врачом. Думаю, что Коперник-старший все-таки был удачливым купцом, так как вряд ли бы сестра влиятельного каноника, дочь председателя городского суда, вышла замуж за простого крестьянина. Словом, он хорошо устроился, и даже избирался городским судьей. У него родилось четверо детей: старший, Андрей, две дочери, и младший, названный, как и отец, Николаем.

– Хорошо, – снова вмешался Владимир Михайлович, – Коперника называют великим польским ученым, – а был ли он вообще поляком?

– На этот вопрос приходится ответить тоже вопросом: а кого следует считать поляком? Того, в чьих жилах течет польская кровь, или кто родился в Польше, или кто внес вклад в историю страны и ее культуру? Исследователь жизни нашего героя отмечал: «Вопрос об этнической принадлежности остается предметом довольно-таки бесперспективной дискуссии». То, что отец переселился из Кракова, еще ни о чем не говорит: в Кракове жило много немцев. Семья Ватценроде, из которой вышла мать Коперника, несомненно, была немецкой. 

Когда-то в Падуанском, кажется, университете Николай назвал себя поляком – но можно ли это считать признаком национальности? «Поляк» в устах студента того времени означало лишь «человек, приехавший из Польши», и вряд ли более того. А в дипломе, выданном в университете, написано: «Николай Коперник из Пруссии». Для полноты картины отметим лишь, что не обнаружено ни одного документа, написанного Коперником на польском языке, а писал он на латыни и на немецком, переводил с греческого. Более того, бытует мнение (не знаю, насколько обоснованное), что Коперник не владел польским языком.

К продолжению